What Is The Line Spectrum
vi.3: Line Spectra and the Bohr Model
- Page ID
- 21730
- To know the relationship between atomic spectra and the electronic structure of atoms.
The concept of the photon emerged from experimentation with thermal radiation, electromagnetic radiation emitted as the result of a source'southward temperature, which produces a continuous spectrum of energies.The photoelectric effect provided indisputable evidence for the beingness of the photon and thus the particle-like behavior of electromagnetic radiations. Withal, more direct testify was needed to verify the quantized nature of energy in all thing. In this section, nosotros describe how observation of the interaction of atoms with visible lite provided this evidence.
Line Spectra
Although objects at loftier temperature emit a continuous spectrum of electromagnetic radiations, a different kind of spectrum is observed when pure samples of private elements are heated. For example, when a high-voltage electrical belch is passed through a sample of hydrogen gas at low pressure, the resulting private isolated hydrogen atoms caused past the dissociation of Hii emit a red light. Different blackbody radiation, the colour of the light emitted past the hydrogen atoms does non depend greatly on the temperature of the gas in the tube. When the emitted low-cal is passed through a prism, only a few narrow lines of particular wavelengths, called a line spectrum, are observed rather than a continuous range of wavelengths (Figure \(\PageIndex{one}\)). The light emitted past hydrogen atoms is red because, of its four characteristic lines, the almost intense line in its spectrum is in the red portion of the visible spectrum, at 656 nm. With sodium, however, we observe a yellow color because the most intense lines in its spectrum are in the xanthous portion of the spectrum, at well-nigh 589 nm.


Such emission spectra were observed for many other elements in the late 19th century, which presented a major challenge because classical physics was unable to explicate them. Part of the explanation is provided by Planck's equation: the observation of simply a few values of λ (or \( u \)) in the line spectrum meant that only a few values of Due east were possible. Thus the energy levels of a hydrogen atom had to be quantized; in other words, simply states that had sure values of free energy were possible, or allowed. If a hydrogen cantlet could have whatsoever value of free energy, then a continuous spectrum would have been observed, similar to blackbody radiation.
In 1885, a Swiss mathematics instructor, Johann Balmer (1825–1898), showed that the frequencies of the lines observed in the visible region of the spectrum of hydrogen fit a elementary equation that tin can be expressed as follows:
\[ u=constant\; \left ( \dfrac{ane}{2^{2}}-\dfrac{one}{due north^{^{2}}} \right ) \label{vi.3.1} \]
where n = 3, four, five, six. Every bit a effect, these lines are known as the Balmer series. The Swedish physicist Johannes Rydberg (1854–1919) afterwards restated and expanded Balmer'south consequence in the Rydberg equation:
\[ \dfrac{1}{\lambda }=\Re\; \left ( \dfrac{1}{n^{2}_{1}}-\dfrac{1}{n^{2}_{two}} \right ) \label{6.iii.ii} \]
where \(n_1\) and \(n_2\) are positive integers, \(n_2 > n_1\), and \( \Re \) the Rydberg constant, has a value of i.09737 × 107 chiliad−1.
A mathematics teacher at a secondary school for girls in Switzerland, Balmer was 60 years old when he wrote the paper on the spectral lines of hydrogen that made him famous.

Balmer published only one other paper on the topic, which appeared when he was 72 years old.
Like Balmer's equation, Rydberg's uncomplicated equation described the wavelengths of the visible lines in the emission spectrum of hydrogen (with n 1 = 2, northward 2 = 3, 4, 5,…). More important, Rydberg's equation as well predicted the wavelengths of other series of lines that would be observed in the emission spectrum of hydrogen: i in the ultraviolet (n 1 = 1, n 2 = 2, 3, 4,…) and one in the infrared (n 1 = three, n ii = 4, 5, 6). Unfortunately, scientists had non yet adult any theoretical justification for an equation of this form.
Bohr'south Model
In 1913, a Danish physicist, Niels Bohr (1885–1962; Nobel Prize in Physics, 1922), proposed a theoretical model for the hydrogen atom that explained its emission spectrum. Bohr'due south model required only one assumption: The electron moves around the nucleus in circular orbits that tin can take only certain allowed radii. Rutherford's before model of the atom had also assumed that electrons moved in circular orbits around the nucleus and that the atom was held together by the electrostatic attraction betwixt the positively charged nucleus and the negatively charged electron. Although we now know that the assumption of circular orbits was wrong, Bohr's insight was to advise that the electron could occupy only sure regions of space.
Using classical physics, Niels Bohr showed that the energy of an electron in a particular orbit is given by
\[ E_{n}=\dfrac{-\Re hc}{n^{ii}} \label{6.3.iii} \]
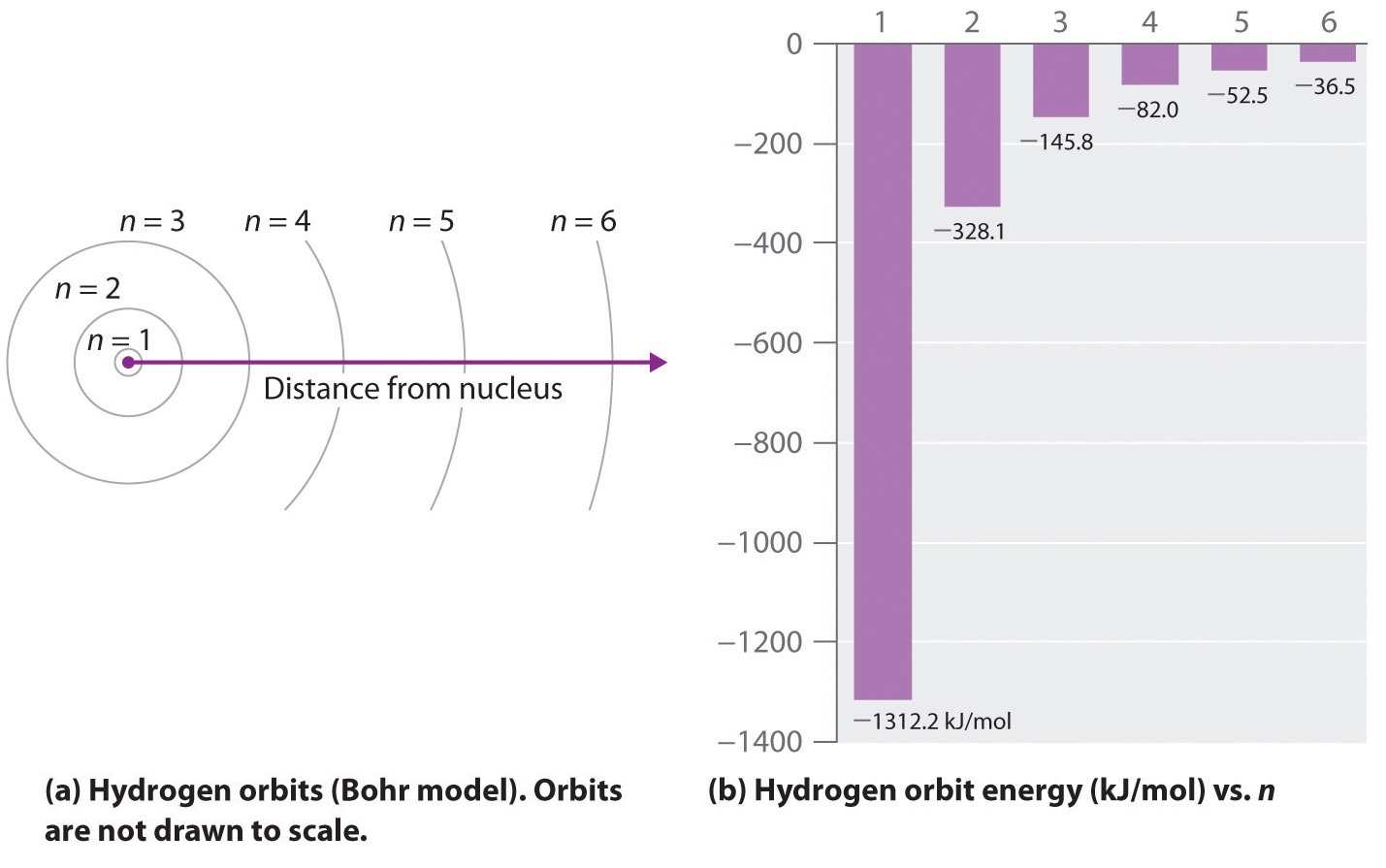
where \( \Re \) is the Rydberg abiding, h is Planck's constant, c is the speed of light, and north is a positive integer respective to the number assigned to the orbit, with due north = i respective to the orbit closest to the nucleus. In this model n = ∞ corresponds to the level where the free energy holding the electron and the nucleus together is nil. In that level, the electron is unbound from the nucleus and the cantlet has been separated into a negatively charged (the electron) and a positively charged (the nucleus) ion. In this state the radius of the orbit is also space. The cantlet has been ionized.
During the Nazi occupation of Denmark in World State of war Ii, Bohr escaped to the United States, where he became associated with the Atomic Energy Projection.

In his final years, he devoted himself to the peaceful awarding of diminutive physics and to resolving political problems arising from the development of atomic weapons.
As north decreases, the energy holding the electron and the nucleus together becomes increasingly negative, the radius of the orbit shrinks and more energy is needed to ionize the atom. The orbit with north = ane is the lowest lying and about tightly leap. The negative sign in Equation \(\ref{vi.3.3}\) indicates that the electron-nucleus pair is more tightly bound (i.e. at a lower potential energy) when they are near each other than when they are far autonomously. Considering a hydrogen atom with its one electron in this orbit has the lowest possible free energy, this is the ground state (the nearly stable arrangement of electrons for an element or a compound) for a hydrogen atom. As n increases, the radius of the orbit increases; the electron is farther from the proton, which results in a less stable arrangement with higher potential energy (Figure \(\PageIndex{2a}\)). A hydrogen atom with an electron in an orbit with n > 1 is therefore in an excited land, defined equally any organisation of electrons that is higher in energy than the ground state. When an atom in an excited country undergoes a transition to the footing state in a process called decay, it loses energy by emitting a photon whose energy corresponds to the divergence in energy betwixt the 2 states (Figure \(\PageIndex{1}\)).

Then the difference in free energy (\(ΔE\)) betwixt any two orbits or free energy levels is given by \( \Delta Due east=E_{n_{i}}-E_{n_{2}} \) where n 1 is the final orbit and n 2 the initial orbit. Substituting from Bohr's equation (Equation \ref{6.iii.three}) for each energy value gives
\[\brainstorm{align*} \Delta East &=E_{concluding}-E_{initial} \\[4pt] &=-\dfrac{\Re hc}{n_{2}^{two}}-\left ( -\dfrac{\Re hc}{n_{1}^{2}} \right ) \\[4pt] &=-\Re hc\left ( \dfrac{1}{n_{2}^{2}} - \dfrac{ane}{n_{i}^{2}}\right ) \characterization{6.3.four} \terminate{align*} \]
If \(n_2 > n_1\), the transition is from a higher free energy state (larger-radius orbit) to a lower free energy country (smaller-radius orbit), every bit shown by the dashed arrow in part (a) in Figure \(\PageIndex{3}\). Substituting \(hc/λ\) for \(ΔE\) gives
\[ \Delta E = \dfrac{hc}{\lambda }=-\Re hc\left ( \dfrac{1}{n_{2}^{2}} - \dfrac{one}{n_{i}^{2}}\right ) \label{6.3.5} \]
Canceling \(hc\) on both sides gives
\[ \dfrac{ane}{\lambda }=-\Re \left ( \dfrac{1}{n_{2}^{ii}} - \dfrac{1}{n_{ane}^{2}}\right ) \label{half-dozen.3.6} \]
Except for the negative sign, this is the aforementioned equation that Rydberg obtained experimentally. The negative sign in Equations \(\ref{6.three.5}\) and \(\ref{6.3.half dozen}\) indicates that energy is released as the electron moves from orbit \(n_2\) to orbit \(n_1\) because orbit \(n_2\) is at a higher energy than orbit \(n_1\). Bohr calculated the value of \(\Re\) from cardinal constants such as the charge and mass of the electron and Planck'south constant and obtained a value of 1.0974 × x7 one thousand−1, the aforementioned number Rydberg had obtained by analyzing the emission spectra.
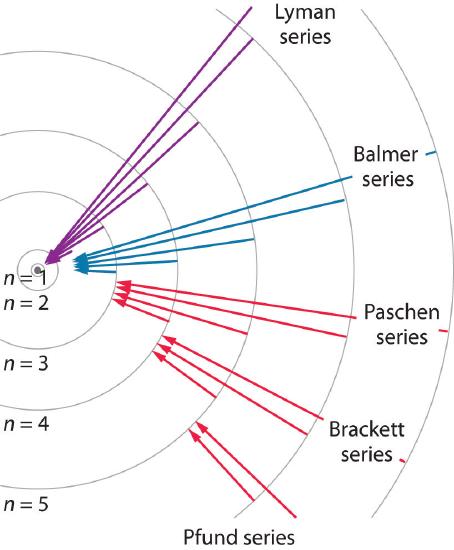
We can now understand the physical basis for the Balmer series of lines in the emission spectrum of hydrogen (\(\PageIndex{3b}\)); the lines in this series correspond to transitions from college-free energy orbits (north > 2) to the second orbit (northward = 2). Thus the hydrogen atoms in the sample accept absorbed energy from the electrical discharge and decayed from a college-energy excited state (n > ii) to a lower-energy state (n = 2) by emitting a photon of electromagnetic radiation whose energy corresponds exactly to the deviation in energy between the two states (Figure \(\PageIndex{3a}\)). The n = iii to northward = ii transition gives ascension to the line at 656 nm (red), the n = iv to northward = 2 transition to the line at 486 nm (green), the due north = 5 to n = 2 transition to the line at 434 nm (blue), and the n = 6 to north = 2 transition to the line at 410 nm (violet). Because a sample of hydrogen contains a large number of atoms, the intensity of the diverse lines in a line spectrum depends on the number of atoms in each excited state. At the temperature in the gas belch tube, more atoms are in the n = 3 than the north ≥ 4 levels. Consequently, the n = iii to n = 2 transition is the well-nigh intense line, producing the feature cherry-red color of a hydrogen discharge (Figure \(\PageIndex{1a}\)). Other families of lines are produced by transitions from excited states with n > 1 to the orbit with n = 1 or to orbits with n ≥ 3. These transitions are shown schematically in Figure \(\PageIndex{iv}\)
The Bohr Atom: The Bohr Atom, YouTube(opens in new window) [youtu.exist]
In gimmicky applications, electron transitions are used in timekeeping that needs to exist exact. Telecommunications systems, such as cell phones, depend on timing signals that are accurate to inside a millionth of a 2d per twenty-four hour period, as are the devices that control the U.s. ability grid. Global positioning organisation (GPS) signals must be accurate to within a billionth of a second per 24-hour interval, which is equivalent to gaining or losing no more than one second in i,400,000 years. Quantifying time requires finding an event with an interval that repeats on a regular ground.
To achieve the accuracy required for modern purposes, physicists have turned to the atom. The current standard used to calibrate clocks is the cesium cantlet. Supercooled cesium atoms are placed in a vacuum bedroom and bombarded with microwaves whose frequencies are carefully controlled. When the frequency is exactly right, the atoms absorb enough free energy to undergo an electronic transition to a higher-energy country. Disuse to a lower-energy country emits radiations. The microwave frequency is continually adapted, serving as the clock's pendulum.
In 1967, the second was defined as the duration of 9,192,631,770 oscillations of the resonant frequency of a cesium atom, chosen the cesium clock. Research is currently under way to develop the next generation of atomic clocks that promise to exist even more authentic. Such devices would allow scientists to monitor vanishingly faint electromagnetic signals produced by nerve pathways in the encephalon and geologists to measure variations in gravitational fields, which cause fluctuations in time, that would aid in the discovery of oil or minerals.
The so-called Lyman series of lines in the emission spectrum of hydrogen corresponds to transitions from various excited states to the due north = 1 orbit. Calculate the wavelength of the lowest-energy line in the Lyman serial to iii significant figures. In what region of the electromagnetic spectrum does it occur?
Given: lowest-energy orbit in the Lyman series
Asked for: wavelength of the lowest-energy Lyman line and corresponding region of the spectrum
Strategy:
- Substitute the appropriate values into Equation \ref{vi.three.2} (the Rydberg equation) and solve for \(\lambda\).
- Utilise Effigy 2.ii.1 to locate the region of the electromagnetic spectrum respective to the calculated wavelength.
Solution:
We tin use the Rydberg equation to calculate the wavelength:
\[ \dfrac{1}{\lambda }=-\Re \left ( \dfrac{ane}{n_{2}^{2}} - \dfrac{1}{n_{one}^{2}}\right ) \nonumber \]
A For the Lyman series, n 1 = 1. The lowest-energy line is due to a transition from the n = 2 to n = 1 orbit because they are the closest in energy.
\[ \dfrac{ane}{\lambda }=-\Re \left ( \dfrac{ane}{n_{2}^{2}} - \dfrac{1}{n_{ane}^{2}}\correct )=1.097\times thou^{-1}\left ( \dfrac{1}{i}-\dfrac{1}{4} \right )=8.228 \times x^{six}\; m^{-1} \nonumber \]
It turns out that spectroscopists (the people who study spectroscopy) utilize cm-one rather than m-one as a common unit. Wavelength is inversely proportional to free energy only frequency is direct proportional as shown by Planck's formula, \(E=h u\).
Spectroscopists often talk about energy and frequency equally equivalent. The cm-1 unit is particularly convenient. The infrared range is roughly 200 - 5,000 cm-1, the visible from 11,000 to 25.000 cm-i and the UV between 25,000 and 100,000 cm-ane. The units of cm-1 are called wavenumbers, although people oftentimes verbalize it as inverse centimeters. We tin can convert the answer in function A to cm-1.
\[ \widetilde{ u} =\dfrac{i}{\lambda }=8.228\times ten^{6}\cancel{thousand^{-1}}\left (\dfrac{\cancel{m}}{100\;cm} \right )=82,280\: cm^{-1} \nonumber \]
and
\[\lambda = 1.215 \times x^{−7}\; chiliad = 122\; nm \nonumber \]
This emission line is called Lyman blastoff. It is the strongest atomic emission line from the sun and drives the chemistry of the upper temper of all the planets, producing ions past stripping electrons from atoms and molecules. It is completely absorbed past oxygen in the upper stratosphere, dissociating O2 molecules to O atoms which react with other Oii molecules to form stratospheric ozone.
B This wavelength is in the ultraviolet region of the spectrum.
The Pfund series of lines in the emission spectrum of hydrogen corresponds to transitions from higher excited states to the n = 5 orbit. Calculate the wavelength of the second line in the Pfund serial to three significant figures. In which region of the spectrum does it prevarication?
- Reply
-
iv.65 × xthree nm; infrared
Bohr'southward model of the hydrogen atom gave an exact caption for its observed emission spectrum. The post-obit are his key contributions to our understanding of atomic construction:
Unfortunately, Bohr could not explain why the electron should exist restricted to particular orbits. As well, despite a great bargain of tinkering, such as assuming that orbits could be ellipses rather than circles, his model could not quantitatively explain the emission spectra of whatever chemical element other than hydrogen (Effigy \(\PageIndex{5}\)). In fact, Bohr's model worked just for species that contained just i electron: H, He+, Li2 +, and and so forth. Scientists needed a fundamental alter in their way of thinking about the electronic construction of atoms to advance across the Bohr model.

The Free energy States of the Hydrogen Atom
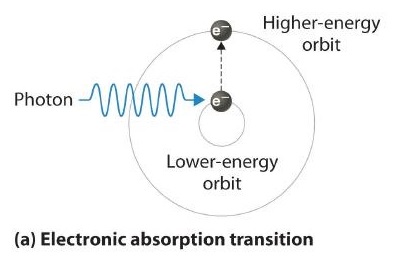
Thus far nosotros take explicitly considered only the emission of lite by atoms in excited states, which produces an emission spectrum (a spectrum produced by the emission of light by atoms in excited states). The converse, absorption of light past basis-state atoms to produce an excited state, can also occur, producing an absorption spectrum (a spectrum produced by the absorption of lite by footing-state atoms).
When an atom emits light, it decays to a lower energy country; when an cantlet absorbs lite, it is excited to a higher free energy state.
If white lite is passed through a sample of hydrogen, hydrogen atoms absorb energy as an electron is excited to college energy levels (orbits with n ≥ 2). If the light that emerges is passed through a prism, it forms a continuous spectrum with black lines (corresponding to no light passing through the sample) at 656, 468, 434, and 410 nm. These wavelengths correspond to the n = 2 to n = 3, n = ii to n = iv, n = 2 to n = 5, and due north = 2 to n = 6 transitions. Whatever given element therefore has both a characteristic emission spectrum and a characteristic absorption spectrum, which are essentially complementary images.
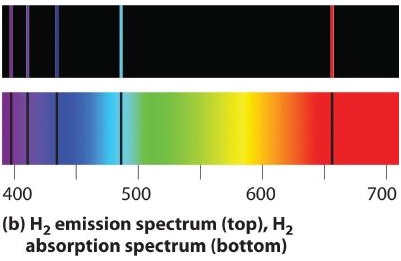
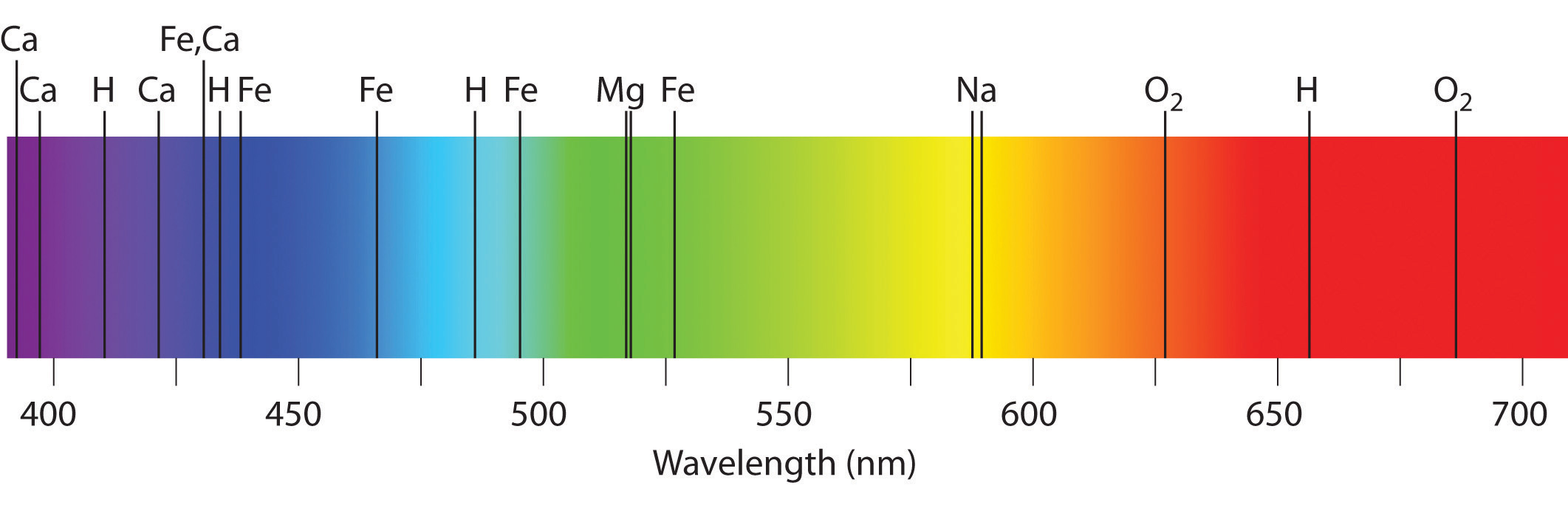
Emission and assimilation spectra grade the ground of spectroscopy, which uses spectra to provide information about the structure and the composition of a substance or an object. In item, astronomers use emission and absorption spectra to make up one's mind the limerick of stars and interstellar matter. As an instance, consider the spectrum of sunlight shown in Figure \(\PageIndex{vii}\) Because the sun is very hot, the light it emits is in the form of a continuous emission spectrum. Superimposed on it, however, is a series of nighttime lines due primarily to the absorption of specific frequencies of light by cooler atoms in the outer atmosphere of the sun. By comparison these lines with the spectra of elements measured on Earth, we now know that the sun contains large amounts of hydrogen, atomic number 26, and carbon, along with smaller amounts of other elements. During the solar eclipse of 1868, the French astronomer Pierre Janssen (1824–1907) observed a set of lines that did not match those of any known element. He suggested that they were due to the presence of a new element, which he named helium, from the Greek helios, pregnant "sun." Helium was finally discovered in uranium ores on Earth in 1895. Blastoff particles are helium nuclei. Blastoff particles emitted by the radioactive uranium selection up electrons from the rocks to form helium atoms.
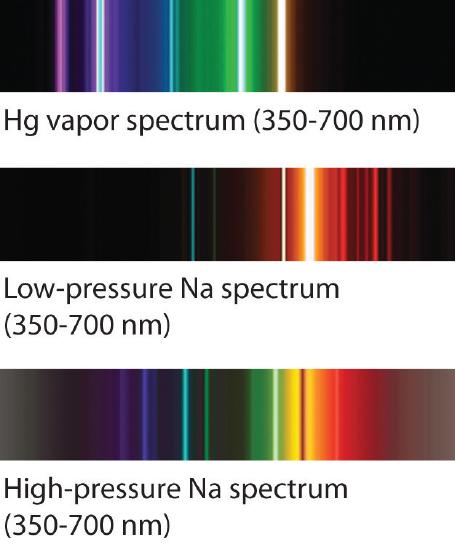
The familiar red color of neon signs used in advertisement is due to the emission spectrum of neon shown in part (b) in Effigy \(\PageIndex{5}\). Similarly, the bluish and yellow colors of certain street lights are caused, respectively, by mercury and sodium discharges. In all these cases, an electrical discharge excites neutral atoms to a higher energy state, and light is emitted when the atoms decay to the ground state. In the instance of mercury, most of the emission lines are beneath 450 nm, which produces a blue calorie-free (part (c) in Figure \(\PageIndex{v}\)). In the instance of sodium, the most intense emission lines are at 589 nm, which produces an intense yellow calorie-free.
Summary
In that location is an intimate connectedness between the diminutive construction of an cantlet and its spectral characteristics. Atoms of private elements emit light at only specific wavelengths, producing a line spectrum rather than the continuous spectrum of all wavelengths produced by a hot object. Niels Bohr explained the line spectrum of the hydrogen atom by assuming that the electron moved in circular orbits and that orbits with merely sure radii were immune. Lines in the spectrum were due to transitions in which an electron moved from a higher-energy orbit with a larger radius to a lower-energy orbit with smaller radius. The orbit closest to the nucleus represented the ground country of the cantlet and was most stable; orbits farther away were higher-energy excited states. Transitions from an excited land to a lower-energy state resulted in the emission of light with only a limited number of wavelengths. Atoms tin also absorb light of sure energies, resulting in a transition from the ground land or a lower-energy excited state to a higher-free energy excited state. This produces an absorption spectrum, which has nighttime lines in the same position as the vivid lines in the emission spectrum of an element. Bohr's model revolutionized the understanding of the cantlet just could not explain the spectra of atoms heavier than hydrogen.
Key Concepts
- Electrons can occupy only certain regions of space, called orbits.
- Orbits closer to the nucleus are lower in energy.
- Electrons tin motion from 1 orbit to another by absorbing or emitting energy, giving rise to characteristic spectra.
What Is The Line Spectrum,
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/06%3A_Electronic_Structure_of_Atoms/6.03%3A_Line_Spectra_and_the_Bohr_Model
Posted by: bunchriewhicur.blogspot.com


0 Response to "What Is The Line Spectrum"
Post a Comment